How quants think about risk

A framework for high-risk investing

I’m Som - Chief Investment Officer at Quantbase. I’ve grappled for a long time with the definition of risk - and more importantly, why it matters in investing.

So first off, Quantbase is a quant hedge fund for everyone - we’re pretty clear about our goal to make high-risk investing standardized, in the same way S&P-tracking ETFs have made investing a standardized activity since the 1970s. You want to buy the market? Buy the market. Of course “the market,” since the 70s, has almost always meant the US equity market, or sometimes the global equity market.

So what if you want to buy the market - with a diversified, standardized, passive investment vehicle - but you're looking to take on more risk and aim for a higher return than can be achieved with traditional ETFs? Well, that’s a little bit trickier. What’s a good standard definition of high-risk?

• Is investing in TWTR mid-merger high-risk?

• WallStreetBets-style large options bets on volatile stocks?

• Crypto (monolithically)?

  • Tokens below a certain market cap? At a certain volatility?

  • DeFi?

• Alternative assets with low liquidity that aren’t exchange-traded?

  • NFTs? Wine? Art?

• Gambling? Prediction markets?

• Investing a large percentage of your capital into assets/strategies/opportunities that you don’t know enough about?

Ask your financial advisor about Shiba Inu in your portfolio today.

I mean, like, all of these things. Standardizing high-risk investing turned out to be a pretty grand endeavor, and a really fun problem for us to solve.

So if we’re going to standardize high risk, we’re going to start with a very brief stop in the 1960s, when American economist Harry Markowitz first standardized the definition of risk in finance, with his Modern Portfolio Theory (MPT). If you’re familiar with MPT, I’m not going past a brief mention. If you’re unfamiliar, again I’m not going past a brief mention - you should read more if it piques your interest.

MPT in essence boiled down the returns from any stock into two numbers - the mean return and the variance of returns, the return in each period consisting of the gain (or loss) in price plus any dividends received. Consequently, any portfolio of stocks could then be considered an asset itself based on its mean and variance. Variance is the square of standard deviation, which is synonymous with volatility.

There’s a lot of things we can do with MPT (in many regards, it’s the basis for almost all of modern financial theory), but for the most part there’s two important numbers: mean and volatility of returns.

The layman’s definition for volatility’s pretty easy - number goes up or down a lot, it’s volatile. It’s measured as a percentage: an asset with a daily volatility of 0.3% is on average going to have that much of an absolute difference between the return on a given day and the average return over the time period.

Every asset has an expected mean return and a volatility of returns. You want a higher mean return for a given level of volatility (or lower volatility for a given mean return). So then you want to combine assets together so that the entire portfolio of these assets has the highest mean for some volatility, or the lowest volatility for a given mean return. Easy stuff!

Some of the conclusions and terms MPT gives us:

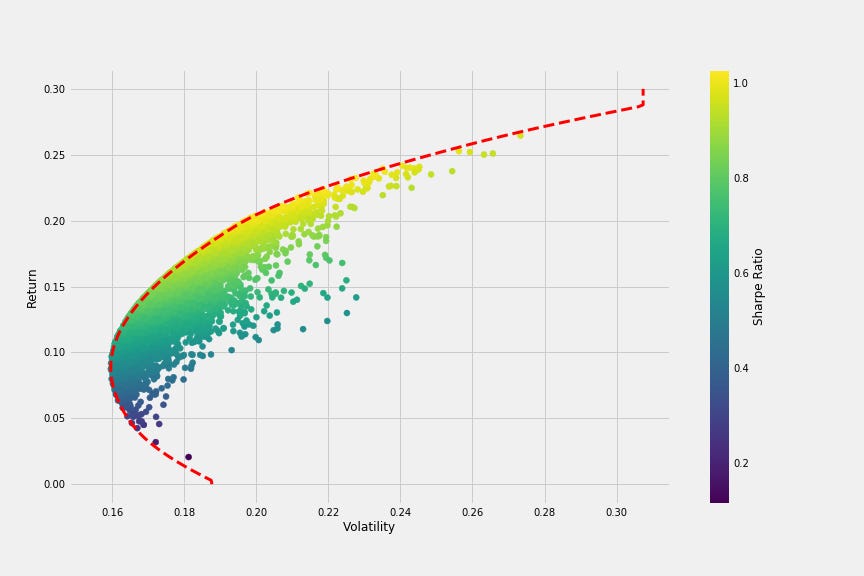
• On the above graph, every dot is a portfolio of assets you can get. The efficient frontier is the line that maximizes return / minimizes volatility (different investors are gonna have different preferences, but all investors want to have a portfolio on that line)

• The better portfolios (the ones on that line) are going to be diversified - have a lot of stocks from the market. The best ones are going to have a little bit of every stock. That’s what buying the market is from a statistical, theoretical level

• There’s no free lunch. To make money, you’ll have to risk it in the form of volatility. To make a lot of money, you’re gonna risk a lot more volatility - that’s why investing for the long term is such a good idea. It dampens the effect of volatility on you because you’re not looking to divest any time close to a near-term downturn

• A good way to measure the unit of risk you’re taking on for every unit of expected return is the Sharpe Ratio. Defined as the expected return of a portfolio (over the risk-free rate - aka subtract the short-term Treasury rate from the return of the portfolio) divided by the volatility. The S&P’s Sharpe cycles around 1.0, so that’s often deemed the ratio to shoot for when constructing portfolios. Below that is worse, above it is better.

Let’s talk about the Sharpe. Because forecasting future returns accurately consistently is very impossible, lots of institutions (should, anyways) maximize their Sharpes by lowering the volatility of their portfolios compared to the benchmark instead of dealing too much with increasing expected returns. It’s the metric we lean on when determining high-risk.

It’s not a perfect metric. It penalizes upward volatility as well as downwards (since higher volatility increases the denominator and makes the ratio lower, which is bad); a long position popping up 50% in a day is rarely a bad thing. We could use the Treynor Ratio (which doesn’t penalize upward volatility), but Sharpe has become pretty much modern parlance.

So there’s that, and we’ll end the MPT dive there. If you’re trying to learn more on the topic, Grinold’s Active Portfolio Management is a classic. Thank you Harry Markowitz for doing all the actual heavy lifting here in defining risk (and winning a Nobel Prize for the effort)!

---

High risk is then just turning the knob on risk.

Here’s how most mutual and hedge funds catered towards institutions (who, because they’ve got gobs of money, are almost always very capital-preserving-esque) might turn that risk knob:

Sharpe Ratio = (Expected Returns) / (Expected Volatility)

Maximize Sharpe by investing in actively- or passively-managed assets, and optimizing to reduce volatility. Denominator goes down, ratio goes up, investors are (maybe) happy. Risk knob turned low.

---

Here’s how some more, ahem, aggressive funds might turn that knob:

Sharpe Ratio = (Expected Returns) / (Expected Volatility)

Push Sharpe by pushing expected returns up by employing a little bit of leverage. Or, push it up by employing teams of researchers to find the right stocks in traditional equity markets to push expected returns up and volatility down. Seems like a generally good deal - these stock-pickers are generally not that good though.

---

The way we think about high-risk investing is by maintaining/maximizing Sharpe, turning the knob on both the numerator and denominator up:

Sharpe Ratio = (Expected Returns) / (Expected Volatility)

We increase expected returns by investing in alternative assets - these are beta portfolios of assets that aren’t traded in traditional exchanges, like cryptocurrencies, wine, NFTs, etc - and correspondingly increase the expected volatility due to the smaller market cap of these assets.

Investing in the S&P might offer an annual Sharpe of 1:

Sharpe Ratio = 10% expected annual return / 10% expected annual volatility

Quantbase portfolios seek to offer the same Sharpe of 1:

Sharpe Ratio = 50% expected annual return / 50% expected annual volatility

So it’s not free money. We’re not promising the moon. It’s passive, semi-responsible, broad-based portfolios, like S&P ETFs, that increase your expected return by being okay with a lot more volatility. The volatility comes from the lack of establishment of the asset class in the traditional world. Crypto, NFTs, and wine have a much higher chance of going to zero than asset classes like US stocks, gold, and real estate. You’re paying for that risk with a higher denominator in the Sharpe ratio. You’re decreasing that risk, though, by diversifying within that asset class (with a Crypto Total Market index, for example), and across alternative asset classes.

Standardizing high-risk for us then, in the early innings of Quantbase anyways, means looking at investments through this admittedly narrow lens. We aim for Sharpe Ratios that mirror the S&P’s Sharpe (beating it is great of course, but we’re not currently focused on optimizing more than a few of portfolios to serve this purpose) - it seems like a good way to look at all these crazy new types of investments with a clear eye and be able to filter through them in a semi-sane way.

Invest in our standardized high-risk funds: